Ecuaciones de Cauchy Riemann (ECR)
Sea: f : D ⊆ → C
Z → f (z)
Z → f (z)
Si ∃ f'(z0)= lim f(z0+Δz) - f(z0)
Δz→0 Δz
entonces:
Re[f'(z0)]= lim Re[ f(z0+Δz) - f(z0) ]
Δz→0 Δz
Im[f'(z0)]= lim Im[ f(z0+Δz) - f(z0) ]
Δz→0 Δz
Sea z0=x0+iy0; Δz=Δx+iΔy
f(z0+Δz) - f(z0) = f((x0+iy0)+(Δx+iΔy))-f(x0+iy0))
Δz Δx+iΔy
=(u((x0+Δx);(y0+Δy))-u(x0;y0))+i(v((x0+Δx);(y0+Δy))-v(x0;y0))
Δx+iΔy
f(z) =u(x,y)+iv(x,y) → Re [f(z0)] = u(x,y) Im[f(z0)] = v(x,y)
S: Δy=0 ; Δx→0
lim (u((x0+Δx);(y0))-u(x0;y0))+i(v((x0+Δx);(y0))-v(x0;y0))
Δx→0 Δx
lim Re[ (u((x0+Δx);(y0))-u(x0;y0)) ] = ∂u = ux Δx→0 Δx ∂x
lim Im[ (v((x0+Δx);(y0))-v(x0;y0)) ] = ∂v = vx Δx→0 Δx ∂x
T: Δx=0 ; Δy→0
lim (u((x0);(y0+Δy))-u(x0;y0))+i(v((x0);(y0+Δy))-v(x0;y0))
Δy→0 iΔy
Re[f'(z0)]= lim (v((x0);(y0+Δy))-v(x0;y0)) = ∂v = vy Δy→0 Δy ∂y
Im[f'(z0)]= lim (u((x0);(y0+Δy))-u(x0;y0)) = ∂u = -uy Δy→0 Δy ∂y
Como ∃ lim entonces:
ux = vy vx = -ux → ECR
TEOREMA:
Sea f(z)=u(x,y)+iv(x,y) una función compleja definida en algún dominio D que contiene a z0 y que tiene primeras derivadas parciales continuas, con respecto a "x" ∧ "y" y satisface las Ecf en z0, entonces f'(z0) existe.
Función Analítica
f(z), función compleja se dice que es función analítica en Z0 ,ssi f(z) es deriva ble para todo z en algún día abierto D de centro Z0, de forma concreta: D:|Z - Z0|<r
Jueves 07/05/2015
Funciones Armónicas
Sea f(z) una función analítica, que satisface las ECR:
∂u = ∂v ^ ∂u= -∂u
∂y ∂x ∂y ∂x
∂2u + ∂2u = 0 ^ ∂2v + ∂2v
∂x2 ∂y2 ∂x2 ∂y2
se dice que u(x,y) ∧ v(x,y) son funciones armonicas
∇2u = ∂2u + ∂2u = 0
∂x2 ∂y2 Ec. de Laplace
∂x2 ∂y2
- u(x,y)^v(x,y) se dice que son funciones conjugadas armónicas una de la otra.
- Toda función f(z)=u(x,y)+iv(x,y) que satisfacen las Ec. de Laplace se llaman FUNCIONES ARMÓNICAS.
- Se puede demostar también:
uxx + uyy =0
vxx + vyy =0
- En física se conocen como ecuaciones de potencial
Lunes 11/05/2015
Funciones Transcendentales
Exponencial
f(z) = exp(z)
f(z)=ez
f(z)=ez
- Propiedades:
- eiy = cos(y) + isen(y)
- e-iy = cos(y) - isen(y)
- ez es una función analítica
- ez +w = ez . ew
- ez ≠0 ; Para todo Z ϵ C
- e-z =e1/z
- ez/w =ez-w
- ez = 1 ↔ z=2π ki
- ez =ew ↔ z=w+2π ki
Logaritmica
f(z) = ln(z)
f(z)=ln(r)+i(θ+2πK)
- Propiedades:
- f(z) =ln(r) + iθ es valor principal
- elogz =z
- log(ez)=z
- log(z.w)=log(z)+log(w)
- log(z/w)=log(z)-log(w)
- log(zr)=r.log(z)
- sea z=x+iy ,con y ≠0 ∧ x≤0, entonces log(z) es analítica
- zw = ewlogz
Trigonomtricas
f(z) = sen(z)
f(z) = cos(z)
- Propiedades:
- sen(z)=(eiz-e-iz )/ 2i
- cos(z) =(eiz+e-iz )/ 2i
- tan(z) = sen(z)/ cos(z)
- cos(x+iy) = cos(x) cosh(y)- sen(x) senh(y)
- sen(x+iy) = sen(x) cosh(y)+ cos(x) senh(y)
- cos(z+2kπ) = cos(z)
- sen(z) ^cos(z) son funciones analíticas
Hiperbolicas
f(z) = senh(z)
f(z) = cosh(z)
- Propiedades:
- senh(z) = (ez-e-z )/2
- cosh(z) = (ez-e-z )/2
- senh(iz)= i sen(z)
- cosh(iz)= cos(z)
- senh(z) ^ cosh(z) son funciones analíticas.
Jueves 14/05/2015
Integración en el plano complejo
- EN EL CASO DE LOS NÚMEROS REALES:
.jpg) Link de la imagen:
Link de la imagen:
Es una integral definida en un intervalo [ a,b ] ⊂ R y que se realiza considerando las sumas de Riemann.
- En el caso de los complejos:
Es una integral de linea a lo largo de la curva r en el plano complejo.
- Las integrales de línea complejas son similares a las integrales de línea de funciones reales de dos variables sobre curvas en el plano.
- En el caso de integrales cerradas se presentan novedades que solo se cumplen para funciones analíticas complejas. Tal es el caso de la INTEGRAL DE CAUCHY y la existencia de las derivadas de orden superior.
Integral indefinida
Si f(z) tiene una anti derivada, podemos evaluar la integral indefinida.
Sea: F ' (z) = f(z), entonces:
∫ f(z) dz = F(z) + c ; c ∈ C
- DEFINICIÓN:
f: [ a, b ] → C , tal que:
f (t) = Re [ f (t) ] + i Im [ f (t) ]
Entonces se define la integral de la forma :
Integrales de linea
; f: D⊆ C → C
z → f (z)
- DEFINICIÓN:
Sea z: [α , β] → R2 ,una función continua, tal que:
r={ z(t) / α ≤ t ≤ β }
Se dice que r es una curva DIFERENCIABLE (suave o que no presenta picos) si se cumple:
z' (t) ≠ 0 ; Para todo t ∈ [α , β]
- DEFINICIÓN:
Curva Suave:
Link de la imagen
PROPIEDADES:
- Si r es una curva suave o suave por intervalos y f(z) es una función continua, entonces existe:
Lunes 18/05/2015
Prueba numero 2
Link de la imagen:
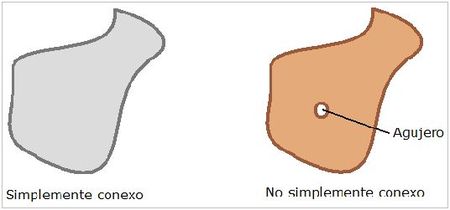
Se dice que D es un conjunto simplemente conexo, si solamente tiene puntos de D( es conexo si no presenta huecos).
Propiedad 6:
Sea r una curva suave a intervalos de z1 a z2 en su dominio simplemente CONEXO D si f(z) es analítica en D y sea F'(z)=f(z) en D entonces:

es independiente de la trayectoria en D.
Siendo γ1 y γ2 so trayectorias diferentes
Propiedad 3:Teorema de deformación
Sea f una funcion analitica en un dominio D excepto en z0 u sean c1^c2 curvas cerradas simples que encierran z0, entonces:
Jueves 25/05/2015
Propiedad 4:Integral de Cauchy
Propiedad 5: Integral de Cauchy para derivadas superiores
Sea f analitica en D, simplemente conexo y sea z0 en D entonces f tiene derivadas de todos los ordenes en z0, por tanto se cumple que.
Links que te podrian interesar:
Parametrizacion de superficies
Ejercicios Resueltos de variable compleja
Curso de analisis complejo
Ejercicios de derivacion
Ejercicios de integracion
Jueves 21/05/2015
Conjunto simplemente conexo
Se dice que D es un conjunto simplemente conexo, si solamente tiene puntos de D( es conexo si no presenta huecos).
Propiedad 6:
Sea r una curva suave a intervalos de z1 a z2 en su dominio simplemente CONEXO D si f(z) es analítica en D y sea F'(z)=f(z) en D entonces:
Integrales Cerradas
Si r es una curva suave cerrada entonces:
r es una curva simple si no presenta entrecruzamientos.
Propiedad 1: TEOREMA DE LA INTEGRAL DE CAUCHY
Sea f(z) una funcion analitica en D, un dominio simplemente conexo y r una curva cerrada simple entonces:
Propiedad 2:
Si f es analitica en un domninio simplemente conexo D, entonces la

es independiente de la trayectoria en D.
Siendo γ1 y γ2 so trayectorias diferentes
Propiedad 3:Teorema de deformación
Sea f una funcion analitica en un dominio D excepto en z0 u sean c1^c2 curvas cerradas simples que encierran z0, entonces:
Jueves 25/05/2015
Propiedad 4:Integral de Cauchy
Si f es analítica en un dominio D simplemente conexo , Sea r cualquier curva cerrada simple en D, que encierre a Zo, entonces:
Propiedad 5: Integral de Cauchy para derivadas superiores
Sea f analitica en D, simplemente conexo y sea z0 en D entonces f tiene derivadas de todos los ordenes en z0, por tanto se cumple que.
Links que te podrian interesar:
Parametrizacion de superficies
Ejercicios Resueltos de variable compleja
Curso de analisis complejo
Ejercicios de derivacion
Ejercicios de integracion







.png)




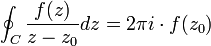

No hay comentarios:
Publicar un comentario