Lunes 1
Sucesiones y series:
Lunes 1
- Las sucesiones y series de variable compleja son similares a las sucesiones y series de variable real.
- El análisis de convergencia se realiza de igual manera que para el caso de la variable real.
- Una serie especialmente para variables complejas es la serie de Laurent
Sucesiones
La sucesión compleja es una función de los números naturales sobre los números complejos.
Propiedades:
si: {zn} --> L y {wn} --> K, se cumple que:
- {zn + wn} --> L + K
- {α zn} --> α L
- {zn * wn} --> L * K
- {zn / wn} --> L / K ; Donde k≠0 al igual que wn≠0
Series
Es la suma de los elementos de una sucesión.
Propiedades:
Series Especiales
Serie Geométrica
Converge si |Z|<1
Diverge si |Z|>1
Serie Armónica
Es divergente
Serie "p"
si: {zn} --> L y {wn} --> K, se cumple que:
- {zn + wn} --> L + K
- {α zn} --> α L
- {zn * wn} --> L * K
- {zn / wn} --> L / K ; Donde k≠0 al igual que wn≠0
Converge si p>1
Diverge si p<=1
Criterios de convergencia
Lunes 8
Series de Taylor
Una función analítica admite un desarrollo mediante una serie de Taylor compleja de forma similar a las funciones reales.
Propiedad 1
Si f es analítica en zo, tiene un desarrollo mediante una serie de Taylor dada por:
Si zo=0 entonces la serie toma el nombre de Serie de Maclaurin y esta dada por:
Jueves 11
Serie de Laurent
Si f(z) no es analítica en z0, entonces no admite desarrollo mediante serie de Taylor.
En este caso se define la serie de Laurent que es propia de funciones de variable compleja.
Sea r1=|z-z0|=r ^ r2=|z-z0|=R; r<R
D={zeC / r<|z-z0|<R}
Teorema:
Sea f(z) analitica en el anillo r<|z-z0|<R, entonces para todo z en este anillo:
Jueves 18
Teorema del residuo
- En la teoría de los números reales consideraba puntos críticos a aquellos valores que toma la variable x, para los cuales f(x) no se define.
- En los números complejos a estos valores que toma "z", tales que f(z) no se define se los denomina singularidades
Singularidades y polos:
Se les denomina a todosd aquellos valores de "z" donde f(z) no se define.
Singularidades:
Si f(z) es analitica en todo el dominio D, siendo D un anillo:
0<|z-z0|<r , excepto en z0. Este z0 constituye una singularidad de f(z).
Polos:
- Si g(z) es una funcion analitica en todo el dominio de D, siendo D:
0<|z-z0|<r, y f(z)=(g(z))/(z-z0)^n
entonces, z0 es un polo de orden "n".
Residuo:
Si la función f(z) tiene un polo en zj. El residuo de f en zj es a-1 y se calcula mediante:
Teorema del residuo:
Si f(z) es analítica en D, excepto en Z1, Z2, ... , Zj; donde f tiene singularidades. Sea γ una curva cerrada suave o suave por intervalos en D que encierra a Z1, Z2, ... , Zj; entonces:
EXPOSICIONES
Lunes 22
Funciones periodicas y ortogonales
Presentacion
Jueves 25
Series de Fourier
Presentacion
Lunes 29
Series de Fourier de funciones pares e impares
Presentacion
Lunes 8
Una función analítica admite un desarrollo mediante una serie de Taylor compleja de forma similar a las funciones reales.
Propiedad 1
Si f es analítica en zo, tiene un desarrollo mediante una serie de Taylor dada por:
Si zo=0 entonces la serie toma el nombre de Serie de Maclaurin y esta dada por:
Jueves 11
Serie de Laurent
Si f(z) no es analítica en z0, entonces no admite desarrollo mediante serie de Taylor.
En este caso se define la serie de Laurent que es propia de funciones de variable compleja.
Sea r1=|z-z0|=r ^ r2=|z-z0|=R; r<R
D={zeC / r<|z-z0|<R}
Teorema:
Sea f(z) analitica en el anillo r<|z-z0|<R, entonces para todo z en este anillo:
Jueves 18
Teorema del residuo
- En la teoría de los números reales consideraba puntos críticos a aquellos valores que toma la variable x, para los cuales f(x) no se define.
- En los números complejos a estos valores que toma "z", tales que f(z) no se define se los denomina singularidades
Singularidades y polos:
Se les denomina a todosd aquellos valores de "z" donde f(z) no se define.
Singularidades:
Si f(z) es analitica en todo el dominio D, siendo D un anillo:
0<|z-z0|<r , excepto en z0. Este z0 constituye una singularidad de f(z).
Polos:
- Si g(z) es una funcion analitica en todo el dominio de D, siendo D:
0<|z-z0|<r, y f(z)=(g(z))/(z-z0)^n
entonces, z0 es un polo de orden "n".
Residuo:
Si la función f(z) tiene un polo en zj. El residuo de f en zj es a-1 y se calcula mediante:
Teorema del residuo:
Si f(z) es analítica en D, excepto en Z1, Z2, ... , Zj; donde f tiene singularidades. Sea γ una curva cerrada suave o suave por intervalos en D que encierra a Z1, Z2, ... , Zj; entonces:
Lunes 22
Funciones periodicas y ortogonales
Presentacion
Jueves 25
Series de FourierPresentacion
Lunes 29
Series de Fourier de funciones pares e imparesPresentacion









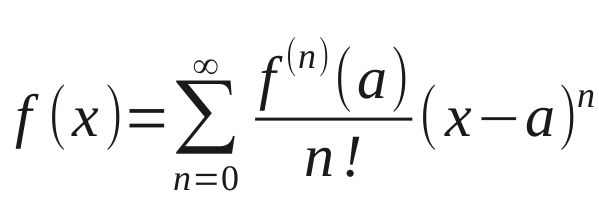







No hay comentarios:
Publicar un comentario